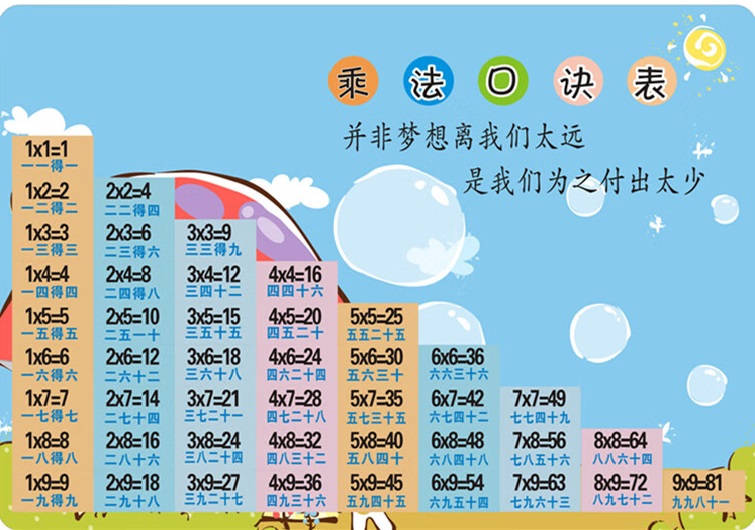
这是一张乘法口诀表,免费,可下载
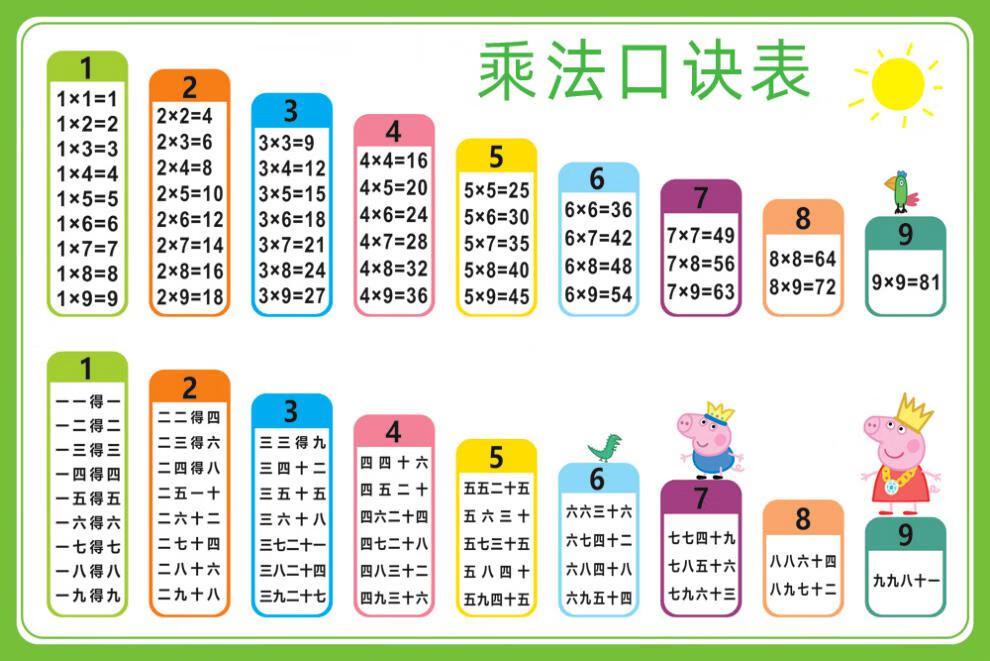
- 乘法口诀表 | 免费可打印乘法图表
- 乘法口诀计算表下载
- 乘法学习AI小帮手
- 乘法表互动练习与教学工具 – 趣味学习乘法的得力助手
- 免费可打印九九乘法表 | 乘法学习工具
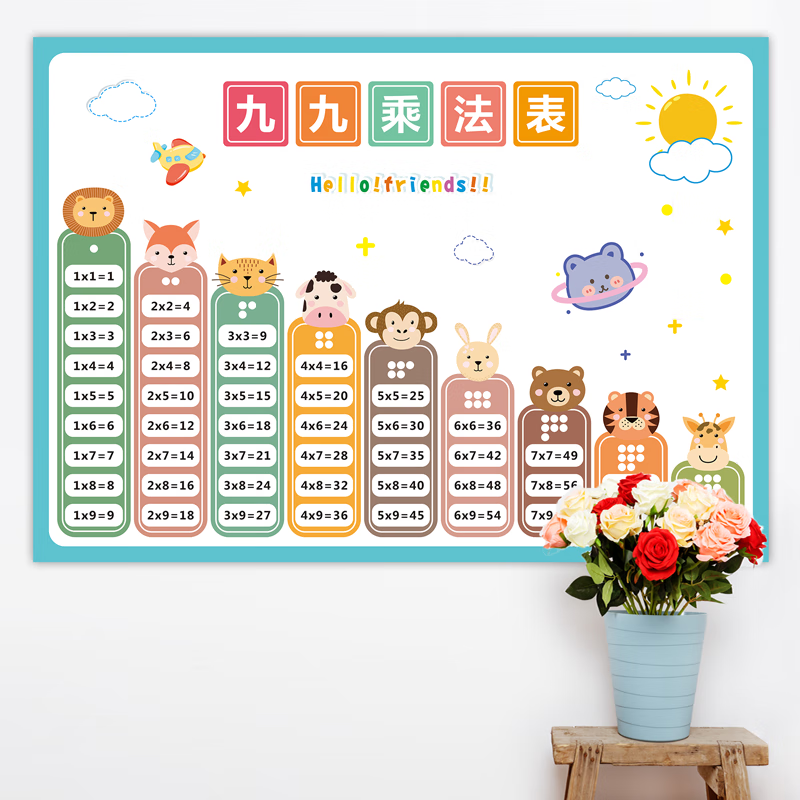
- 动物版乘法口诀表下载
- 可爱版乘法口诀表下载
- 各类乘法
- 家长教乘法
- 小学老师教乘法
- 经典版乘法口诀表下载
- 阳光版乘法口诀表下载
- 除法口诀表下载
类似网站

这是一张乘法口诀表,免费,可下载


这是一张乘法口诀表,免费,可下载

这是一张口诀表,同时包含乘法口诀表,也包含除法口诀表,免费,可下载。
乘法口诀表:从 “1×1 = 1” 到 “9×9 = 81”,涵盖 1 – 9 数字两两相乘的结果,是数学乘法运算的基础记忆内容,帮助快速得出乘法运算答案。比如计算 3×4,依据口诀 “三四十二”,能立刻知道结果是 12 。
除法口诀表:呈现 1 – 9 数字相关的除法运算结果,是乘法口诀表的逆运算。例如,根据乘法口诀 “二四得八”,在除法中 8÷2 = 4,8÷4 = 2 。它有助于理解除法概念,快速计算除法算式。

乘法口诀表在中国有着悠久的历史,最早可追溯到春秋战国时期。它是中国古代数学智慧的结晶,在古代的教育、商业活动等方面都发挥了重要作用。随着时间的推移,乘法口诀表传播到了日本、韩国等周边国家,对这些国家的数学教育也产生了深远影响。在现代数学教育中,它依旧是基础且重要的内容。
理解记忆法:比如在记忆 “三五十五” 时,可以理解为 3 个 5 相加,也就是 5+5+5 = 15 ,这样通过加法运算来理解乘法的含义,能让记忆更深刻。
规律记忆法:观察乘法口诀表,会发现其中存在一些规律。像 9 的乘法口诀,积的十位数字和个位数字相加等于 9 。例如 “二九十八”,1+8 = 9;“三九二十七”,2+7 = 9 。利用这些规律能帮助快速记忆。
故事记忆法:可以编造一些有趣的故事来辅助记忆。比如,孙悟空有 72 般变化,对应 “八九七十二”,这样有趣的故事能让口诀记忆变得轻松愉快。
购物场景:去超市买苹果,每个苹果 2 元,买 5 个苹果需要多少钱?这就用到了 “二五一十” 的乘法口诀,2×5 = 10(元) 。
装修场景:如果要给一个正方形的房间铺地砖,每边铺 6 块,一共需要多少块地砖?利用 “六六三十六”,6×6 = 36(块) 。

如何判断两个数的积是否为偶数或奇数?如果一个整数可以被2整除,那么它就是偶数;反之,如果不能被2整除,那么它就是奇数。
对于两个数a和b,它们的积ab是偶数当且仅当a和b中至少有一个是偶数。这是因为偶数乘以任何数(包括另一个偶数)都是偶数,而奇数乘以任何数(包括另一个奇数)也是偶数。因此,如果a和b中至少有一个是偶数,那么ab一定是偶数;反之,如果a和b都是奇数,那么ab就一定是奇数。

如何快速计算多位数的乘法?一种常用的技巧是“分块法”,即将大数分解成若干个较小的部分,然后分别与另一个数相乘,最后再将结果相加。
例如,要计算3456*789,可以将其拆分为(3000+400+50+6)*789=2364000+115600+39450+4704=2529044。这种方法适用于那些乘积中有较大位数的情况。
另一种方法是“竖式乘法”,即将一位数和两位数对齐,从右到左依次进行相乘,并将结果累加起来。这种方法适用于那些乘积中位数较少的情况。
参考资料:
1. 数学教学网:https://www.shuxuejiaoyu.com/algorithm/multiplication/
2. Khan Academy:https://www.khanacademy.org/math/arithmetic/multiplication-and-fractions/multiplication-tutorial/a/multiplying-2-digit-numbers

可以使用分配律、结合律和交换律来简化乘法计算。
1. 分配律:两个数的和与一个数相乘,等于这两个数分别与这个数相乘再把积相加。
例如:(2+3)×4 = 2×4 + 3×4 = 8 + 12 = 20
2. 结合律:三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积不变。
例如:(2×3)×4 = 6×4 = 24;2×(3×4) = 2×12 = 24
3. 交换律:两个数相乘,交换因数的位置,积不变。
例如:2×3 = 3×2 = 6
参考资料:
1. “乘法运算定律”,百度百科:https://baike.baidu.com/item/%E5%90%8D%E5%8C%BA%E7%AF%87%E5%AE%9A/535224
2. “运算法则”, Khan Academy: https://www.khanacademy.org/math/arithmetic/multiplication-and-division/v/multiplying-mixed-numbers-and-fractions

乘法是一种基本的算术运算,它表示将两个或更多的数加在一起的快捷方式。例如,3 x 4 表示将三个四相加,即 3 + 3 + 3 + 3 = 12。
乘法规则:
1. 任何数与0相乘都得0。
2. 任何数与1相乘都得原数。
3. 一个数与负数相乘得负数,如 5 x -2 = -10。
4. 交换两个因数的位置,积不变,即 a x b = b x a。
5. 有理数乘法的分配律:(a+b) x c = a x c + b x c。
参考资料:
– Khan Academy: https://www.khanacademy.org/math/arithmetic/multiplication-and-fractions/
– Math is Fun: https://www.mathsisfun.com/multiplication.html

1. 什么是乘法?
2. 什么是乘方?
3. 如何理解乘法规则?
4. 如何记忆乘法口诀表?
5. 举例说明乘法的应用。
6. 如何利用乘法公式简化计算?
7. 如何判断两个数的积是否为偶数或奇数?
8. 如何快速计算多位数的乘法?
9. 如何用乘法解决实际生活中的问题?
10. 如何将分数转换为小数并进行乘法运算?

背诵乘法口诀表的方法如下:
1. 从左到右、从上到下顺序记忆,例如2*1=2、2*2=4、3*1=3等。
2. 分类记忆,将一些有规律的数字归类记忆,如2、3、5的倍数等。
3. 利用联想记忆,将数字和生活中的事物相联系,增加记忆的乐趣和效果。
参考资料:
https://www.math.com.cn/primary/jiexue/chuanshu/1679.html

一种常用的乘法口诀表快速记忆法是”竖着背,横着想”。具体步骤如下:
1. 将乘法口诀表竖着看,从左到右依次为1*1=1, 2*1=2, 3*1=3…9*1=9。
2. 然后将第一行的数(即1)作为横坐标,第二行至第十行的数(即2-9)作为纵坐标,得出每个乘积的结果。
3. 接下来将第三行的数作为横坐标,第四行至第十行的数作为纵坐标,得出每个乘积的结果,以此类推,直到第九行和第十行。
4. 在横向上,每个数字的位置代表了它的倍数,例如在第一行中,第一个数字2表示2的倍数,第二个数字5表示5的倍数。
5. 在纵向上,每个数字的位置代表了另一个数字,例如在第三行中,第一个数字3表示3的倍数,第二个数字6表示6的倍数。
通过这种方法,可以快速地记住乘法口诀表,并且可以在实际计算时灵活运用。参考资料:《数学思维训练:趣味乘法口诀表》。

怎么计算两位数乘法?
可以使用列竖式的方法进行计算。具体步骤如下:
1. 将被乘数和乘数分别写在竖式的上方和下方。
2. 从右往左一位一位地相乘,将结果写在竖式下面对应的位置。
3. 计算过程中需要注意进位,即当某一列的乘积超过10时,需要向前进一位。
4. 最后得到的结果就是所求的乘积。
参考资料:
https://www.math.com.cn/primary/jiexingshuji/chujishu/index.html

怎么计算一位数乘法?
一位数乘法是将一个数字与另一个数字相乘的基本算术运算。
例如,要计算5 x 3,您可以按照以下步骤进行:
1. 将3分解为2和1的组合,因为5可以被2整除两次,所以我们将得到10。
2. 将10加到之前的数字(即5)上,得到最终答案15。
参考资料:
https://www.mathsisfun.com/multiplication.html

乘法的性质是什么?
乘法的交换律是:a×b=b×a;
乘法结合律是:(a×b)×c=a×(b×c);
乘法分配律是:a×(b+c)=a×b+a×c

乘法的原理是什么?
乘法是一种基本的算术运算,它表示将一个数与另一个数相乘的过程。乘法原理是这样的:
1. 两个或多个相同的数相乘,结果等于这些数的总和。
2. 将一个数重复加多次,可以使用乘法来简化计算。
3. 乘法满足交换律和结合律,即a*b = b*a和(a*b)*c = a*(b*c)。
参考资料:
– Khan Academy: https://www.khanacademy.org/math/arithmetic/multiplication_and_division
– Math Is Fun: http://mathisfun.com/multiplication.html

乘法的本质是什么?
乘法是一种基本的算术运算,它表示将一个数与另一个数相乘的过程。乘法的本质是重复加法,即将一个数加上自身指定的次数。例如,2 x 3实际上是2 + 2 + 2的结果。
参考资料:
1. Khan Academy: https://www.khanacademy.org/math/arithmetic/multiplication-and-division
2. Math Is Fun: https://www.mathsisfun.com/multiplication.html
3. Purplemath: https://www.purplemath.com/modules/multi.htm