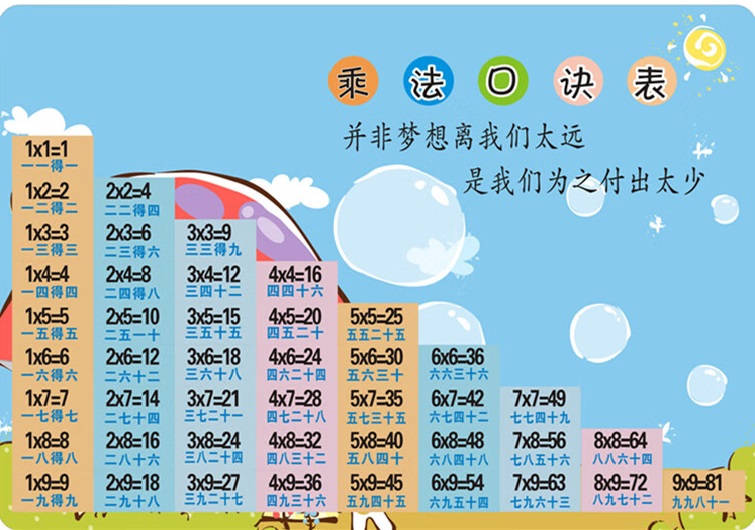
乘法话题广场
-
乘法:家长该怎么教幼儿园小孩乘法
类别:cnFAQ可以通过以下方式教幼儿园小孩乘法:
1. 利用具体的物品进行实物演示,例如让孩子看到一组有三个苹果和两组有四个苹果的图片,然后让他们计算总共有多少个苹果。
2. 制作乘法表格,让孩子通过观察表格中的数据,理解乘法的概念。
3. 利用游戏的方式来教授乘法,例如制作一些包含乘法题目的拼图或益智游戏。参考资料:
– “Teaching Multiplication to Young Children” by National Council of Teachers of Mathematics
– “Multiplication: A Guide for Teaching Students with Learning Disabilities and Difficulties” by Learning Disabilities Association of America
- 乘法口诀表 | 免费可打印乘法图表
- 乘法口诀计算表下载
- 乘法学习AI小帮手
- 乘法表互动练习与教学工具 – 趣味学习乘法的得力助手
- 免费可打印九九乘法表 | 乘法学习工具
- 动物版乘法口诀表下载
- 可爱版乘法口诀表下载
- 各类乘法
- 家长教乘法
- 小学老师教乘法
- 经典版乘法口诀表下载
- 阳光版乘法口诀表下载
- 除法口诀表下载
类似网站

-
乘法:怎么计算矩阵乘法
类别:cnFAQ怎么计算矩阵乘法?在进行矩阵乘法时,需要确保第一个矩阵的列数与第二个矩阵的行数相等。
以下是一个简单的示例:
设A为2×3的矩阵,B为3×2的矩阵:
“`
A = [[1, 2, 3],
[4, 5, 6]]B = [[7, 8],
[9, 10],
[11, 12]]“`那么,AB的结果C将是一个2×2的矩阵,可以通过以下方式计算:
“`
C = [[(1*7 + 2*9 + 3*11), (1*8 + 2*10 + 3*12)],
[(4*7 + 5*9 + 6*11), (4*8 + 5*10 + 6*12)]]“`所以,结果矩阵C是:
“`
C = [[58, 64],
[139, 154]]“`
参考资料:
– 维基百科 – 矩阵乘法
– Khan Academy – Matrix Multiplication
- 乘法口诀表 | 免费可打印乘法图表
- 乘法口诀计算表下载
- 乘法学习AI小帮手
- 乘法表互动练习与教学工具 – 趣味学习乘法的得力助手
- 免费可打印九九乘法表 | 乘法学习工具
- 动物版乘法口诀表下载
- 可爱版乘法口诀表下载
- 各类乘法
- 家长教乘法
- 小学老师教乘法
- 经典版乘法口诀表下载
- 阳光版乘法口诀表下载
- 除法口诀表下载
类似网站

-
乘法:怎么计算向量乘法
类别:cnFAQ怎么计算向量乘法?
向量的点积(内积)是通过将两个向量对应元素相乘并求和来计算的。
数学公式表示为:
a·b = |a||b|cosθ
其中,a 和 b 是要进行点积的两个向量,|a| 和 |b| 分别表示它们的模(长度),θ 表示它们之间的夹角。
例如,假设我们有两个二维向量 a = (1, 2) 和 b = (3, 4),那么它们的点积可以通过以下方式计算:
a·b = (1 * 3) + (2 * 4) = 3 + 8 = 11
另外,如果你正在使用 Python,你可以使用 numpy 库中的 dot 函数来进行向量的点积运算:
“`python
import numpy as npa = np.array([1, 2])
b = np.array([3, 4])dot_product = np.dot(a, b)
print(dot_product) # 输出 11.0
“`
参考资料:
– https://en.wikipedia.org/wiki/Dot_product
– https://numpy.org/doc/stable/reference/generated/numpy.dot.html
- 乘法口诀表 | 免费可打印乘法图表
- 乘法口诀计算表下载
- 乘法学习AI小帮手
- 乘法表互动练习与教学工具 – 趣味学习乘法的得力助手
- 免费可打印九九乘法表 | 乘法学习工具
- 动物版乘法口诀表下载
- 可爱版乘法口诀表下载
- 各类乘法
- 家长教乘法
- 小学老师教乘法
- 经典版乘法口诀表下载
- 阳光版乘法口诀表下载
- 除法口诀表下载
类似网站

-
乘法:怎么计算分数乘法
类别:cnFAQ怎么计算分数乘法?要计算分数乘法,可以按照以下步骤操作:
1. 将分子相乘得到新的分子。
2. 将分母相乘得到新的分母。
3. 如果新的分母为零,则结果为无穷大;如果新的分子为零且新的分母不为零,则结果为零。参考资料:
1. 《中学数学教材》
2. Khan Academy(https://www.khanacademy.org/math/arithmetic/fractions-and-division/multiplying-fractions/a/multiplying-fractions)
- 乘法口诀表 | 免费可打印乘法图表
- 乘法口诀计算表下载
- 乘法学习AI小帮手
- 乘法表互动练习与教学工具 – 趣味学习乘法的得力助手
- 免费可打印九九乘法表 | 乘法学习工具
- 动物版乘法口诀表下载
- 可爱版乘法口诀表下载
- 各类乘法
- 家长教乘法
- 小学老师教乘法
- 经典版乘法口诀表下载
- 阳光版乘法口诀表下载
- 除法口诀表下载
类似网站

-
乘法:怎么计算小数乘法
类别:cnFAQ怎么计算小数乘法?
小数乘法的计算方法是将小数转化为分数或者整数进行相乘,然后再将结果化为小数形式。例如,0.5乘以0.3可以先将两个小数都转化为分数,即0.5=1/2,0.3=3/10,然后进行相乘得到1/2乘以3/10=3/20,最后将结果化为小数形式,即3/20=0.15。
参考资料:
– 《小学数学教学设计与实践》(赵春燕、王维新编著)
– Khan Academy – Multiplying Decimals (https://www.khanacademy.org/math/arithmetic/fraction-arithmetic/multiplying-fractions/v/multiplying-decimals)
- 乘法口诀表 | 免费可打印乘法图表
- 乘法口诀计算表下载
- 乘法学习AI小帮手
- 乘法表互动练习与教学工具 – 趣味学习乘法的得力助手
- 免费可打印九九乘法表 | 乘法学习工具
- 动物版乘法口诀表下载
- 可爱版乘法口诀表下载
- 各类乘法
- 家长教乘法
- 小学老师教乘法
- 经典版乘法口诀表下载
- 阳光版乘法口诀表下载
- 除法口诀表下载
类似网站

-
乘法:怎么计算三位数乘法
类别:cnFAQ怎么计算三位数乘法?要计算三位数乘法,可以使用列竖式的方法。
例如:
234
x 567首先,将第一个数的个位数(4)与第二个数的每一位相乘,得到的结果写在下面的一行。然后,将第一个数的十位数(3)与第二个数的每一位相乘,得到的结果加到前面结果的后面。最后,将第一个数的百位数(2)与第二个数的每一位相乘,得到的结果加到前面结果的后面。
所以:
234
x 567= 12048 + 13920 + 12708
= 38676
参考资料:
1. 数学基础教程:乘法运算。
2. 教育部制定的《义务教育数学课程标准》中关于乘法运算的相关内容。
- 乘法口诀表 | 免费可打印乘法图表
- 乘法口诀计算表下载
- 乘法学习AI小帮手
- 乘法表互动练习与教学工具 – 趣味学习乘法的得力助手
- 免费可打印九九乘法表 | 乘法学习工具
- 动物版乘法口诀表下载
- 可爱版乘法口诀表下载
- 各类乘法
- 家长教乘法
- 小学老师教乘法
- 经典版乘法口诀表下载
- 阳光版乘法口诀表下载
- 除法口诀表下载
类似网站

-
乘法:怎么计算两位数乘法
类别:cnFAQ怎么计算两位数乘法?
可以使用列竖式的方法进行计算。具体步骤如下:
1. 将被乘数和乘数分别写在竖式的上方和下方。
2. 从右往左一位一位地相乘,将结果写在竖式下面对应的位置。
3. 计算过程中需要注意进位,即当某一列的乘积超过10时,需要向前进一位。
4. 最后得到的结果就是所求的乘积。参考资料:
https://www.math.com.cn/primary/jiexingshuji/chujishu/index.html
- 乘法口诀表 | 免费可打印乘法图表
- 乘法口诀计算表下载
- 乘法学习AI小帮手
- 乘法表互动练习与教学工具 – 趣味学习乘法的得力助手
- 免费可打印九九乘法表 | 乘法学习工具
- 动物版乘法口诀表下载
- 可爱版乘法口诀表下载
- 各类乘法
- 家长教乘法
- 小学老师教乘法
- 经典版乘法口诀表下载
- 阳光版乘法口诀表下载
- 除法口诀表下载
类似网站

-
乘法:怎么计算一位数乘法
类别:cnFAQ怎么计算一位数乘法?
一位数乘法是将一个数字与另一个数字相乘的基本算术运算。
例如,要计算5 x 3,您可以按照以下步骤进行:
1. 将3分解为2和1的组合,因为5可以被2整除两次,所以我们将得到10。
2. 将10加到之前的数字(即5)上,得到最终答案15。
参考资料:
https://www.mathsisfun.com/multiplication.html
- 乘法口诀表 | 免费可打印乘法图表
- 乘法口诀计算表下载
- 乘法学习AI小帮手
- 乘法表互动练习与教学工具 – 趣味学习乘法的得力助手
- 免费可打印九九乘法表 | 乘法学习工具
- 动物版乘法口诀表下载
- 可爱版乘法口诀表下载
- 各类乘法
- 家长教乘法
- 小学老师教乘法
- 经典版乘法口诀表下载
- 阳光版乘法口诀表下载
- 除法口诀表下载
类似网站

-
乘法:乘法的性质是什么
类别:cnFAQ乘法的性质是什么?
乘法的交换律是:a×b=b×a;
乘法结合律是:(a×b)×c=a×(b×c);
乘法分配律是:a×(b+c)=a×b+a×c
- 乘法口诀表 | 免费可打印乘法图表
- 乘法口诀计算表下载
- 乘法学习AI小帮手
- 乘法表互动练习与教学工具 – 趣味学习乘法的得力助手
- 免费可打印九九乘法表 | 乘法学习工具
- 动物版乘法口诀表下载
- 可爱版乘法口诀表下载
- 各类乘法
- 家长教乘法
- 小学老师教乘法
- 经典版乘法口诀表下载
- 阳光版乘法口诀表下载
- 除法口诀表下载
类似网站

-
乘法:乘法的原理是什么
类别:cnFAQ乘法的原理是什么?
乘法是一种基本的算术运算,它表示将一个数与另一个数相乘的过程。乘法原理是这样的:
1. 两个或多个相同的数相乘,结果等于这些数的总和。
2. 将一个数重复加多次,可以使用乘法来简化计算。
3. 乘法满足交换律和结合律,即a*b = b*a和(a*b)*c = a*(b*c)。
参考资料:
– Khan Academy: https://www.khanacademy.org/math/arithmetic/multiplication_and_division
– Math Is Fun: http://mathisfun.com/multiplication.html
- 乘法口诀表 | 免费可打印乘法图表
- 乘法口诀计算表下载
- 乘法学习AI小帮手
- 乘法表互动练习与教学工具 – 趣味学习乘法的得力助手
- 免费可打印九九乘法表 | 乘法学习工具
- 动物版乘法口诀表下载
- 可爱版乘法口诀表下载
- 各类乘法
- 家长教乘法
- 小学老师教乘法
- 经典版乘法口诀表下载
- 阳光版乘法口诀表下载
- 除法口诀表下载
类似网站

-
乘法:乘法的本质是什么
类别:cnFAQ乘法的本质是什么?
乘法是一种基本的算术运算,它表示将一个数与另一个数相乘的过程。乘法的本质是重复加法,即将一个数加上自身指定的次数。例如,2 x 3实际上是2 + 2 + 2的结果。
参考资料:
1. Khan Academy: https://www.khanacademy.org/math/arithmetic/multiplication-and-division
2. Math Is Fun: https://www.mathsisfun.com/multiplication.html
3. Purplemath: https://www.purplemath.com/modules/multi.htm
- 乘法口诀表 | 免费可打印乘法图表
- 乘法口诀计算表下载
- 乘法学习AI小帮手
- 乘法表互动练习与教学工具 – 趣味学习乘法的得力助手
- 免费可打印九九乘法表 | 乘法学习工具
- 动物版乘法口诀表下载
- 可爱版乘法口诀表下载
- 各类乘法
- 家长教乘法
- 小学老师教乘法
- 经典版乘法口诀表下载
- 阳光版乘法口诀表下载
- 除法口诀表下载
类似网站

-
乘法:乘法是什么
类别:cnFAQ乘法是一种基本的算术运算,它表示将两个或更多的数相乘以得到一个结果。
例如,2 x 3 = 6,这意味着如果你有两份3,你可以将它们放在一起得到6。
参考资料:
1. Khan Academy: https://www.khanacademy.org/math/arithmetic/multiplication-and-division
2. Math Is Fun: http://mathisfun.comMultiplication.html
- 乘法口诀表 | 免费可打印乘法图表
- 乘法口诀计算表下载
- 乘法学习AI小帮手
- 乘法表互动练习与教学工具 – 趣味学习乘法的得力助手
- 免费可打印九九乘法表 | 乘法学习工具
- 动物版乘法口诀表下载
- 可爱版乘法口诀表下载
- 各类乘法
- 家长教乘法
- 小学老师教乘法
- 经典版乘法口诀表下载
- 阳光版乘法口诀表下载
- 除法口诀表下载
类似网站

-
乘法:小孩子为什么要学乘法
类别:cnFAQ孩子学习乘法可以帮助他们理解和计算数量关系,这对于他们的数学能力和逻辑思维能力的培养非常重要。
参考资料:
1. National Council of Teachers of Mathematics (NCTM). (2000). Principles and Standards for School Mathematics. Reston, VA: Author.
2. Stigler, J. W., & Hiebert, E. F. (1999). The Teaching Gap: Why Our Children Don’t Learn as Much as They Should and What We Can Do About It. New York: Free Press.
- 乘法口诀表 | 免费可打印乘法图表
- 乘法口诀计算表下载
- 乘法学习AI小帮手
- 乘法表互动练习与教学工具 – 趣味学习乘法的得力助手
- 免费可打印九九乘法表 | 乘法学习工具
- 动物版乘法口诀表下载
- 可爱版乘法口诀表下载
- 各类乘法
- 家长教乘法
- 小学老师教乘法
- 经典版乘法口诀表下载
- 阳光版乘法口诀表下载
- 除法口诀表下载
类似网站